menu
home
publications
research
talks
teaching

Research

Tikhonov regularization of monotone operator dynamics

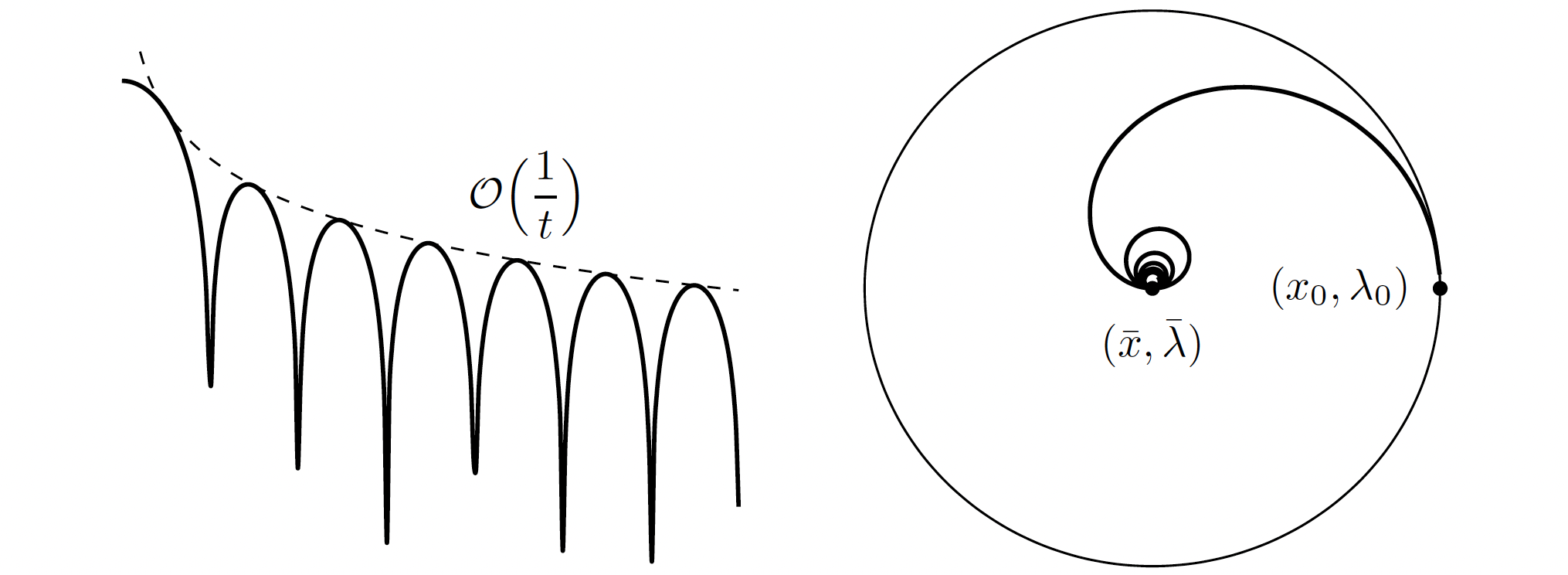
We investigate the asymptotic properties of evolution equations governed by a monotone operator combined with Tikhonov regularization. Under suitable conditions on the Tikhonov terms, we show that the solutions of the regularized dynamics strongly converge toward the element of least norm within the set of zeros of the monotone operator. Furthermore, we derive sharp asymptotic decay rate estimates for the solutions and their velocities. We complement our study by deriving the corresponding results with respect to the so-called viscosity curve.

alt text 

Dynamical approaches to linearly constrained convex minimization

Our research pertains to the dynamical viewpoint of solving linearly constrained convex minimization problems with a particular focus on the classical Arrow–Hurwicz differential system and its extensions. We investigate the asymptotic properties of the differential systems and provide conditions for which their solutions converge toward a saddle point of the Lagrangian associated with the convex minimization problems. In addition, we present asymptotic estimates on the decay of the solutions and the primal-dual gap function measured in terms of the Lagrangian.

alt text 

Distributed coordination algorithms for convex minimization

We consider continuous-time coordination algorithms for networks of agents that seek to collectively solve convex minimization problems with an inherent distributed structure. Decentralized algorithmic approaches to solve these optimization problems yield various advantages over centralized solvers, including reduced communication and computational overhead at a single point via spatially distributed processors, robustness against malfunctions, or the ability to quickly react to changes. Our objective is to synthesize distributed coordination algorithms that allow each agent to find their own component of the optimal solution vector. This setup substantially differs from consensus-based distributed optimization where agents agree on the entire optimal solution vector. We also seek to provide algorithm performance guarantees by way of characterizing the convergence rate of the network state towards the optimal solution.

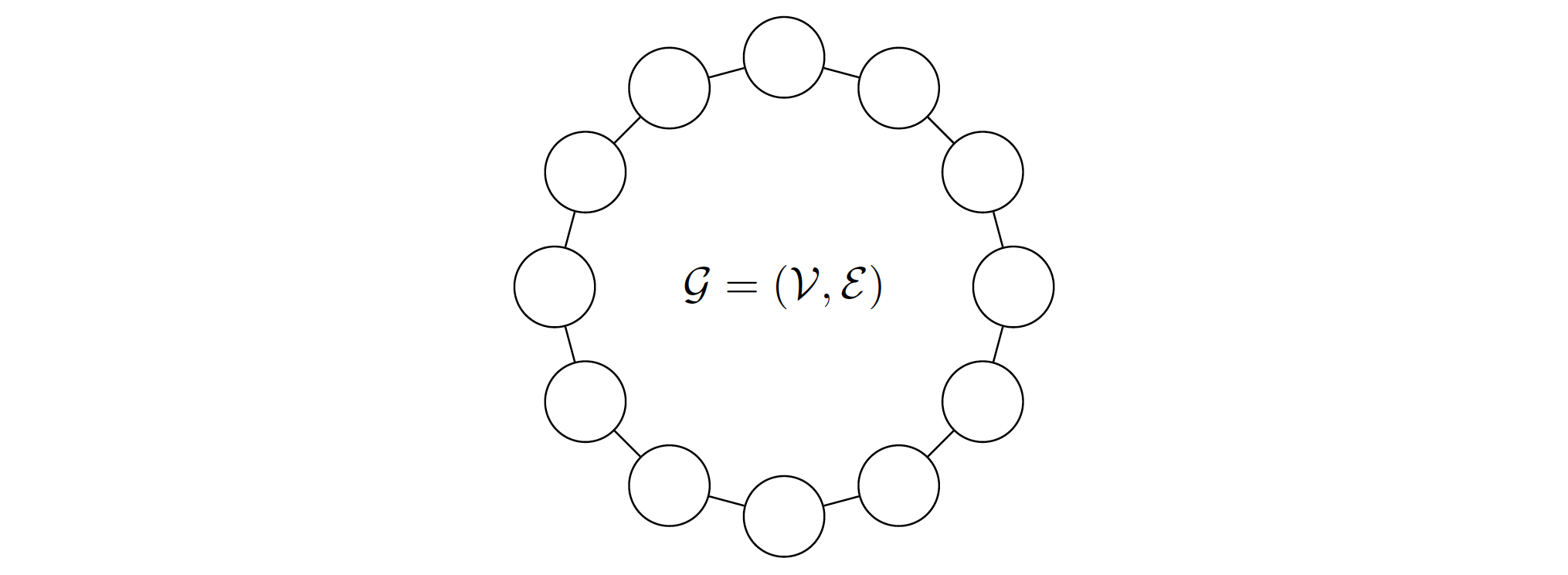alt text